Minimum Spanning Tree(MST)는 무방향 그래프에서의 모든 Vertex들을 연결하는 Edge들의 집합중에서 어떠한 Cycle도 발생하지 않고 Edge의 Weight합이 최소가 되는 집합입니다.

하나의 그래프에서 MST는 하나 혹은 여러개 일 수도 있습니다. 또한 n개의 Vertex를 가지는 MST에서 Edge갯수는 n-1개가 됩니다.

Edge의 Weight합이 최소가 되기 때문에 도로건설, 통신설비 연결, 수도배관 연결, 라우팅 경로 선택 등등 다방면으로 활용될 수 있습니다. MST를 구성하는 알고리즘에는 여러가지가 있지만 여기서는 자주 언급되는 Prim 알고리즘 과 Kruskal 알고리즘을 살펴보고 python으로 구현해 보도록 하겠습니다. 두 알고리즘 모두 Greedy 알고리즘에 속합니다.

또한 두 알고리즘 모두 변의 개수를 E, 꼭짓점의 개수를 V라고 했을 때 \(O(ElogV)\)의 시간복잡도를 가집니다.

Graph 자료구조

MST를 구성하기 위해 사용될 그래프 자료 구조를 먼저 살펴 보도록 하겠습니다. 딕셔너리 vertices는 그래프상의 각각의 Vertex에 대한 Vertex 오브젝트를 가지고 있습니다. 그리고 Vertex 오브젝트는 이웃하는 Vertex 오브젝트와 그에 대한 각각의 Weight에 값을 가집니다.
또한 Kruskal 알고리즘 구현시 편리하도록 edges라는 리스트를 따로 두어 Edge들의 정보를 모아 놓았습니다.

이제 Prim 알고리즘부터 살펴보겠습니다. MST 알고리즘 구현시 가장 주의해야 할 사항은 Cycle이 생기면 안된다는 점입니다.

Prim 알고리즘

Prim 알고리즘은 힙 자료구조를 사용합니다. 힙은 완전이진트리의 일종으로 부모노드가 자식노드보다 항상 크다는 성질을 가지고 있습니다. 그렇기 때문에 힙에 데이터를 추가하고 가장 위쪽노드( root노드 )에서 값을 가져온다면 최대힙의 경우 항상 최댓값을 최소힙의경우 항상 최솟값을 꺼내올 수 있습니다.

알고리즘 진행순서는 다음과 같습니다.

1. 지정된 Vertex부터 시작하여 이와 직접적으로 연결된 Vertex들을 힙에 넣어줍니다.
   (이때 이미 방문한 Vertex는 포함시키지 않습니다.)

2. 힙에서 Weight가 가장 작은 값을 꺼내어 방문하지 않았다면 방문Vertex로 지정합니다.

3. 위 1,2과정을 모든 Vertex가 방문될 때까지 반복합니다.

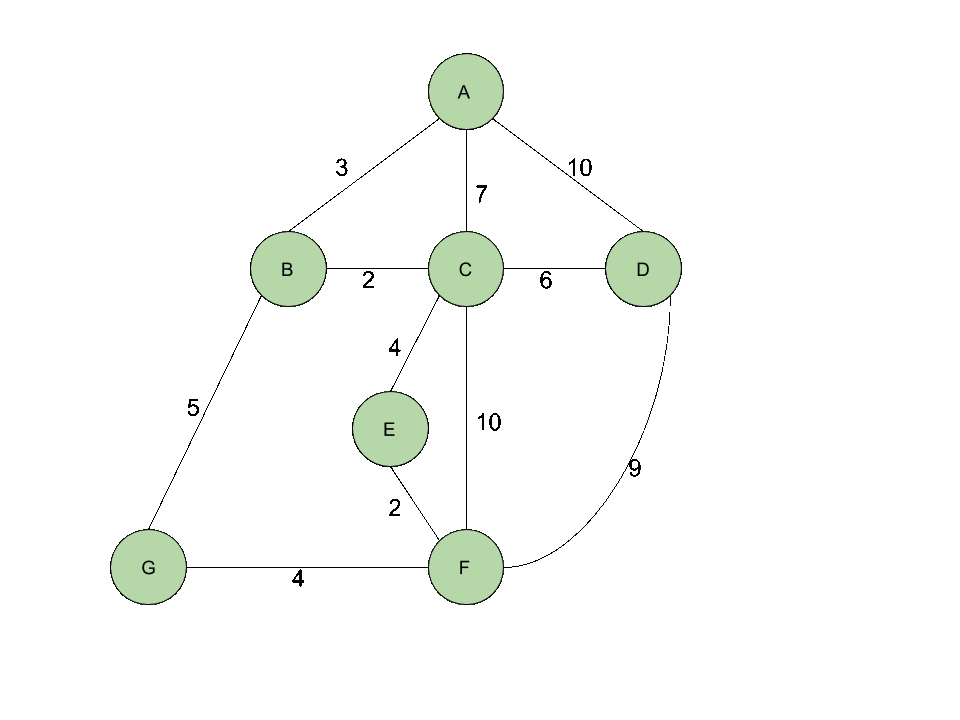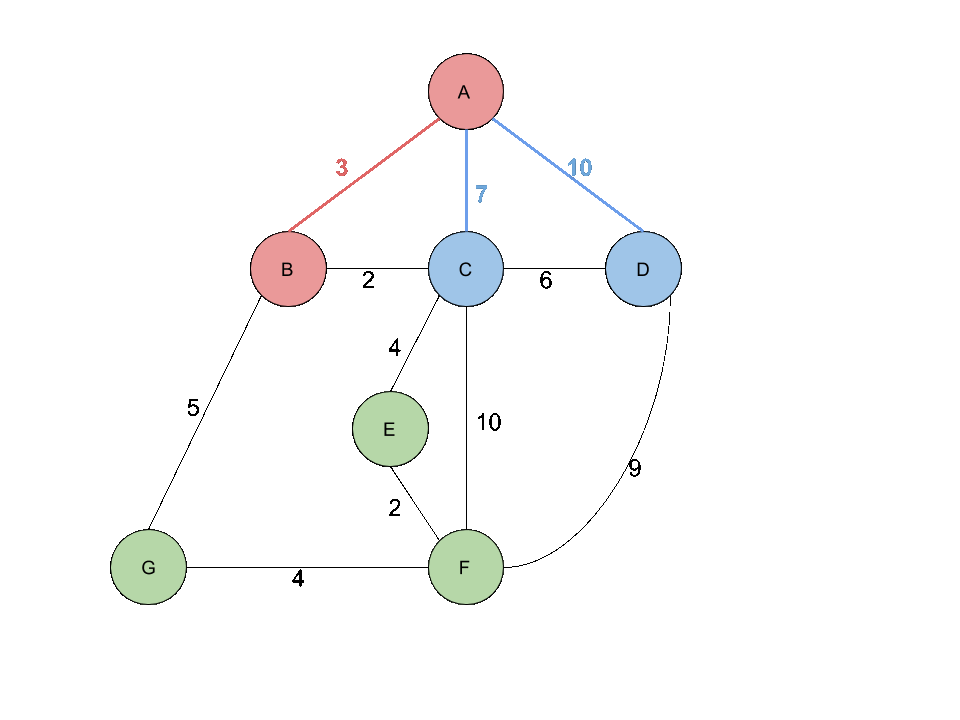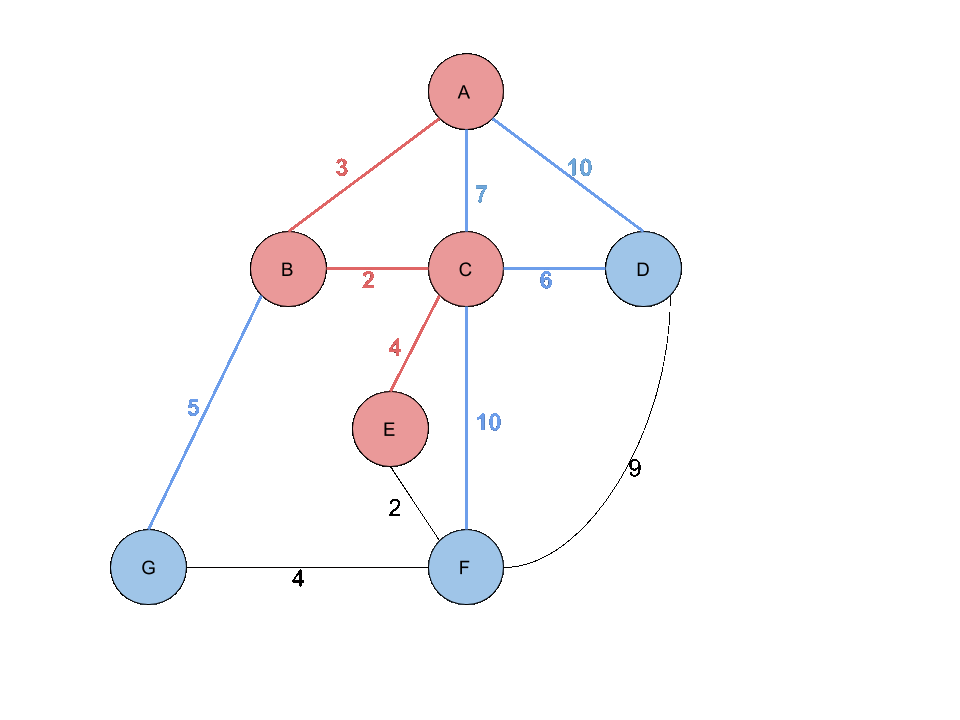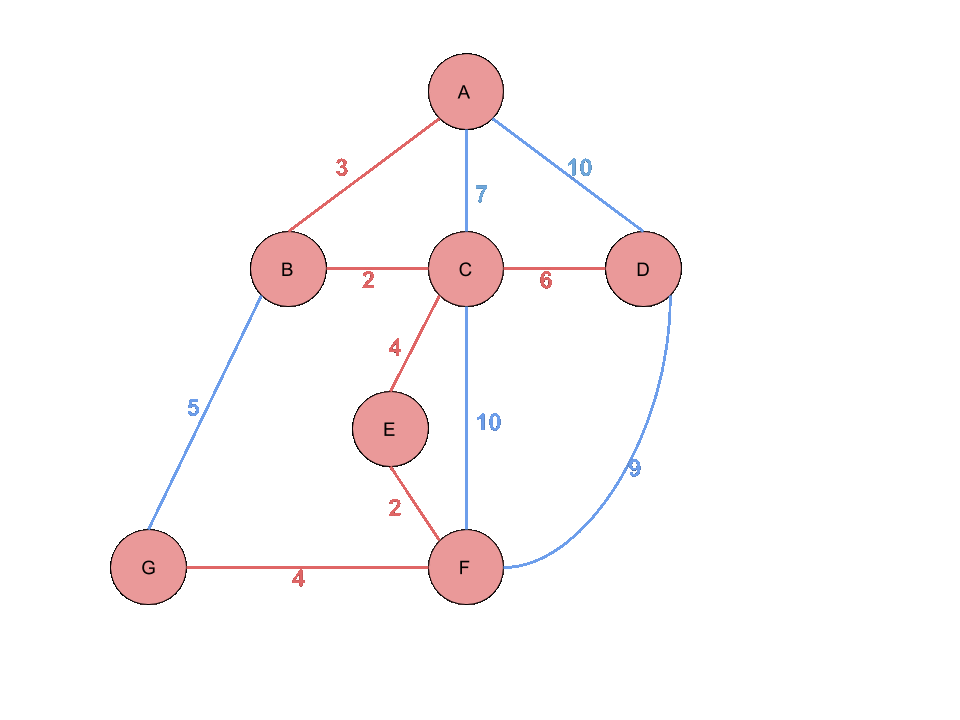
위의 그래프에서 처음 모든 Vertex들은 연두색으로 표시되어 있습니다. Vertex를 발견하게 되면 푸른색으로 표시되고 방문을 하게되면 분홍색으로 표시됩니다.

Vertex A부터 방문하기 시작해서 A의 Edge들인 (A,B),(A,C),(A,D)를 발견하여 최소힙에 넣어줍니다. 그후에 힙의 root 에서 값을 빼오면 최소힙이기 때문에 발견된 Edge중 가장 작은 Weight를 갖는 값인 3이 다음 Edge으로 선택됩니다. (A,B)

그다음 B를 기준으로 위의 과정을 반복하면 됩니다. B에서 발견할 수 있는 이웃노드는 (B,C),(B,G)이므로 힙에 넣어주고 힙에서 가장 작은 값을 가져오면 2가 됩니다. (B,C)

A, B, C를 방문하였으므로 이제 C에서 부터 아직 발견되지 않은 Edge들을 찾으면 (C,E),(C,F),(C,D)가 됩니다. 이들을 힙에 넣고 가장 최솟값을 뽑으면 4가 됩니다. (C,E)

계속해서 E에서 발견되지 않은 Edge을 찾으면 (E,F)가 되고 힙에 넣은뒤에 가장 작은 Weight를 뽑으면 2 (E,F)가 됩니다.

그다음 F에서 발견되지 않은 Edge은 (G,F),(F,D)가 되고 힙에 넣습니다. 이제 더이상 발견되지 않은 Edge이 없기 때문에 모든 노드가 방문될때 까지 힙에서 최솟값들을 뽑아주면 됩니다. 힙에서 Edge (G,F) 와 (C,D)를 순서대로 뽑게되면 모든노드가 방문이 되었습니다. 또한 선택된 Edge의 갯수는 전체 Vertex의 수 - 1이 되는것을 확인할 수 있습니다.

다음은 python으로 구현한 코드입니다. 힙은 heapq 모듈을 사용하여 구현하였습니다.

from graph import Graph
from heapq import heappush, heappop

def mst_prim(graph, start):
    total_cost,mst = 0,[] 
    discovered,explored = [(0,start,start)],set()
    # Started from start position
    while discovered:
        cost,_from,_to = heappop(discovered)
        if _to not in explored:  # If not explored yet then mark as explored
            explored.add(_to)
            total_cost += cost
            mst.append((_from,_to))         
            # Add to the heap certain neighbors which connected to the
            # Vertex and not explored yet
            for neighbor in set(graph.vertices[_to].neighbors) - explored:
                heappush(discovered, (graph.vertices[_to].neighbors[neighbor],
                _to,neighbor))

    return total_cost, mst[1:] # (start, start) is in mst[0] so return without it

Kruskal 알고리즘

Kruskal 알고리즘은 Union-Find(Disjoint-set)라는 자료구조를 이용합니다. Union-Find(Disjoint-set)에 대한 코드는 다음 포스트를 참조하시기 바랍니다.

Kruskal 알고리즘은 Prim 알고리즘에 비해 간단합니다. 알고리즘 진행순서는 다음과 같습니다.

1. Edge들을 Weight가 작은 순으로 정렬을 합니다.
2. 정렬된 Edge들을 하나씩 가져와 Edge에 붙어있는 두 Vertex들을 Union연산을 해줍니다.
3. 이때 두 Vertex에 대한 Find연산결과가 같다면 두 Vertex는 이미 연결 되어 있다고 볼 수 있기 때문에 건너뛰고 2번으로 돌아갑니다.

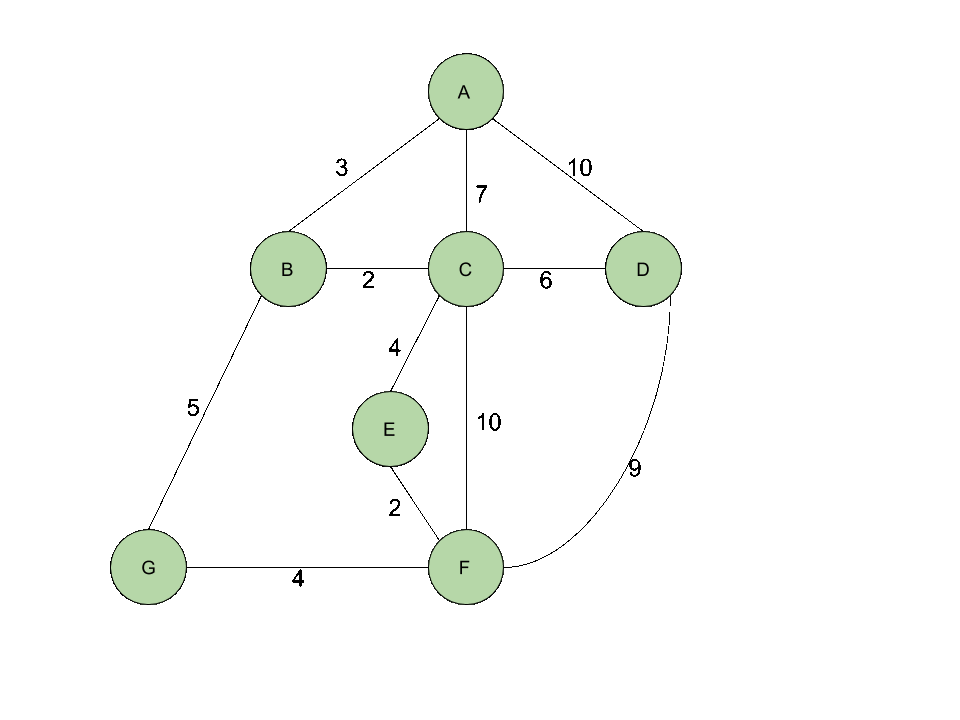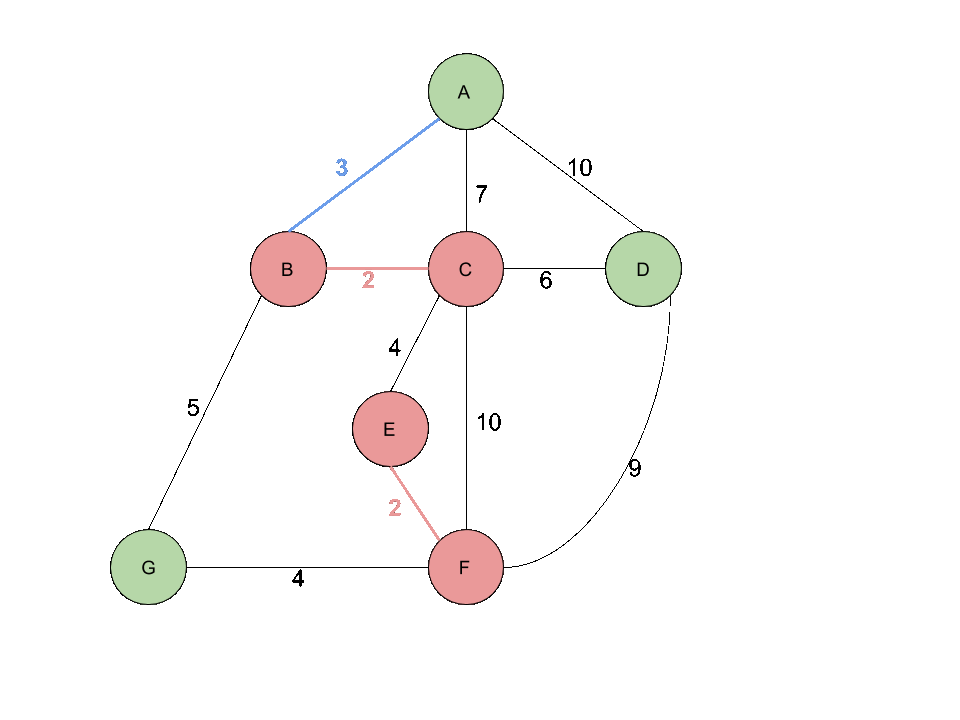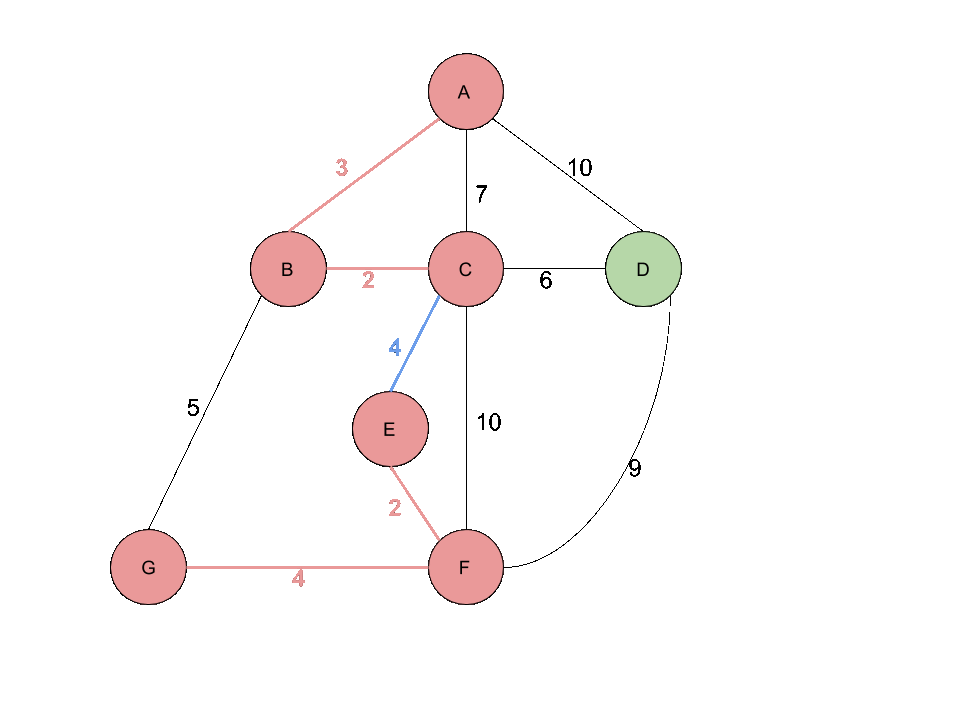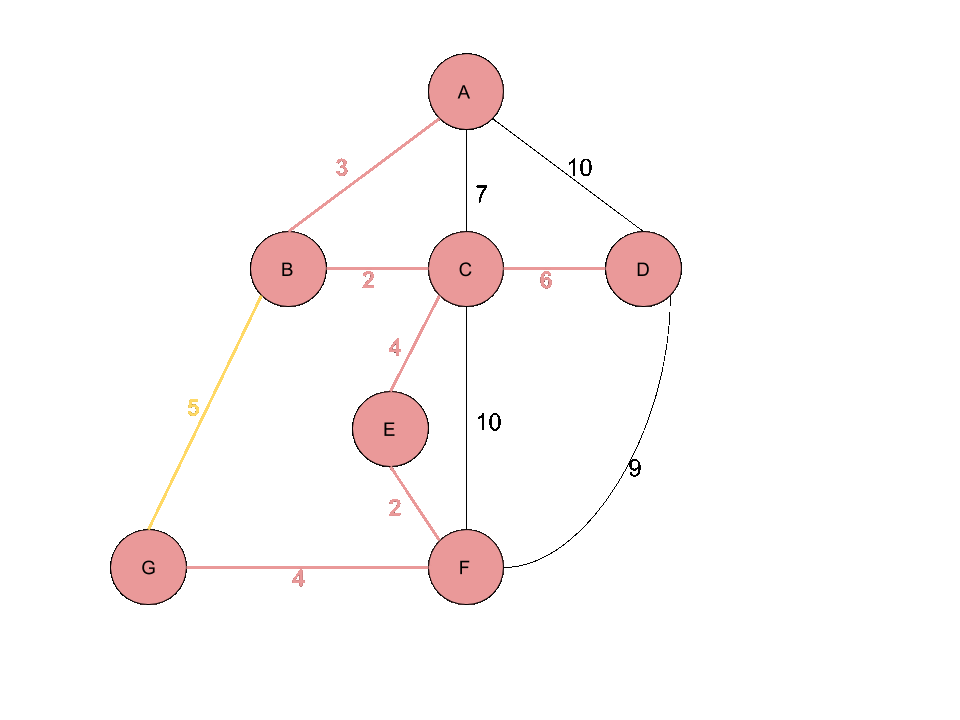
위의 그래프에서 연결이 완료된 Edge은 분홍색으로 표시되고 Cycle이 생기는 Edge은 노란색으로 표시하였습니다. 먼저 Weight순으로 Edge을 오름차순 정렬을 하고나면 가장 Weight가 작은 Edge는 (B,C) 또는 (E,F)입니다.

여기서는 (B,C)가 먼저 나온다고 가정하겠습니다. B 와 C를 Union연산을 하여 하나의 Set으로 만들겠습니다.
계속해서 Weight가 가장 작은 다음 Edge은 (E,F)입니다. E 와 F 또한 Union연산을 하여 하나의 Set으로 만들겠습니다.

그 다음 가장 작은 Edge은 (A,B)입니다. A 와 B를 Union연산을 하여 A,B,C를 하나의 Set으로 만들 수 있습니다.

그다음은 (C,E)와 (G,F)중 (G,F)가 먼저 나온다고 가정하겠습니다. G 와 F를 Union연산하여 E,F,G를 하나의 Set으로 만들었습니다.

그다음은 C 와 E를 Union연산하여 A,B,C,E,F,G를 하나의 Set으로 만들었습니다.

다음에 올 Edge은 (B,G)입니다. 이때 B 와 G를 연결하게 되면 Vertex B,C,E,F,G의 Cycle이 생기게 됩니다. 하지만 이미 B 와 G는 하나의 Set에 포함되어 있기 때문에 Edge (B,G)는 선택되지 않고 다음으로 넘어갑니다.

마지막으로 Edge (C,D)에 경우에 C 와 D를 Union연산을 한 결과 A,B,C,D,E,F,G 모두 하나의 Set이 되어 MST가 완성됩니다.

python으로 구현한 코드는 다음과 같습니다.

from union_find import UnionFind

def mst_kruskal(graph):
    total_cost, mst = 0, []
    u = UnionFind()
    # Sorted by weight
    edges = sorted(graph.get_edges(), key=lambda x: x[2])
    for start, end, weight in edges:
        # If start vertex and end vertex has different parent on Union-Find 
        # structure then joining the two subset
        if u[start] != u[end]:
            u.union(u[start],u[end])
            total_cost += weight
            mst.append((start,end))

    return total_cost, mst

Finally

만약 그래프의 전체 Edge의 개수가 많다면 Prim 알고리즘이 효과적이고 적다면 Kruskal 알고리즘이 더욱 효과적입니다.

다음은 두 알고리즘에 대한 코드를 합해 놓은 것입니다.