Disjoint-Set 자료구조는 많은 서로소 부분 집합들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료 구조입니다. Disjoint-Set은 Union과 Find연산을 제공하며 Union-Find Set이라 불리기도 합니다.

Union과 Find연산은 Linkedlist와 Tree로 구현될 수 있으며 Linkedlist로 구현시에 시간복잡도는 $O(n)$시간이지만 Tree로 구현시 최적화를 통해 최소 $O(\alpha(n))$시간으로 줄일 수 있습니다.
여기서 $O(\alpha(n))$은 아커만 함수(Ackermann function)의 역함수로 5이하의 값을 가지기 때문에 실질적으로 상수 시간에 연산을 수행 할 수 있습니다.

또한 Disjoint-Set 자료구조는 최소신장트리(Minimum Spanning Tree)를 찾는 Kruskal 알고리즘에 사용되기도 하는듯 알아두면 굉장히 유용하게 쓸 수 있습니다.

Kruskal 알고리즘에 대한 코드는 다음 포스트를 참고하시기 바랍니다.

지금 부터 Disjoint-Set에 대하여 예를 통해 살펴보고 python으로 구현해보도록 하겠습니다.

Step by Step

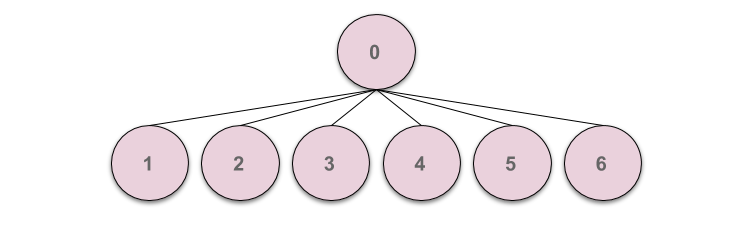
아래의 그림에서와 같이 7개의 부분 집합이 있고 각 부분 집합은 각각의 Parent에 대한 정보를 가지고 있습니다.

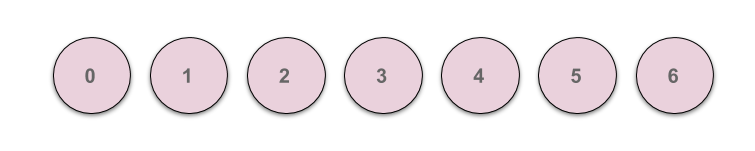초기에는 각 부분집합이 독립이므로 각 부분집합의 Parent는 자기자신이 됩니다.
(Parent[i]=i 이때 i는 각 집합을 나타냅니다.)

이제 집합 (0,1), (3,4), (5,6)을 Union 연산해 보겠습니다.

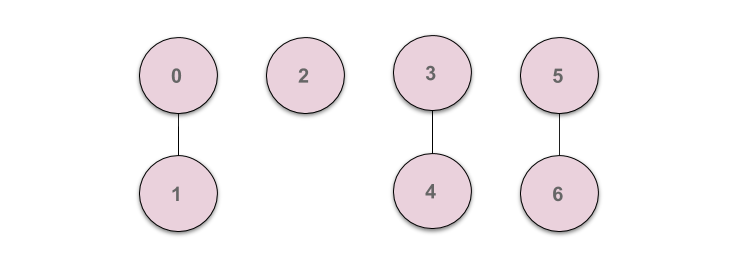
Union에 대한 code는 다음과 같이 나타낼 수 있습니다.

def union(x, y):
  # find function will be return the head of the node
  x,y = find(x),find(y)
  parent[y] = x 

Union 연산은 Find 연산으로 두 집합의 부모를 각각 가져와 부모들을 연결시켜주면 됩니다.

다음은 Find연산에 대한 code입니다.

def find(x):
  # recursively called until find the parent
  if parent[x] == x: return x
  else: return find(parent[x])

Find 연산은 recursive call을 통해 최종 Parent 값을 반환합니다.

계속해서 다음은 (1,2), (3,6)을 Union연산 하는 경우입니다.

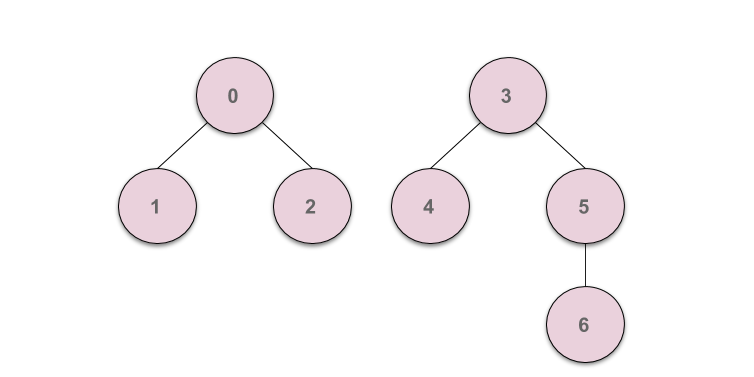
Union, Find 연산의 한계

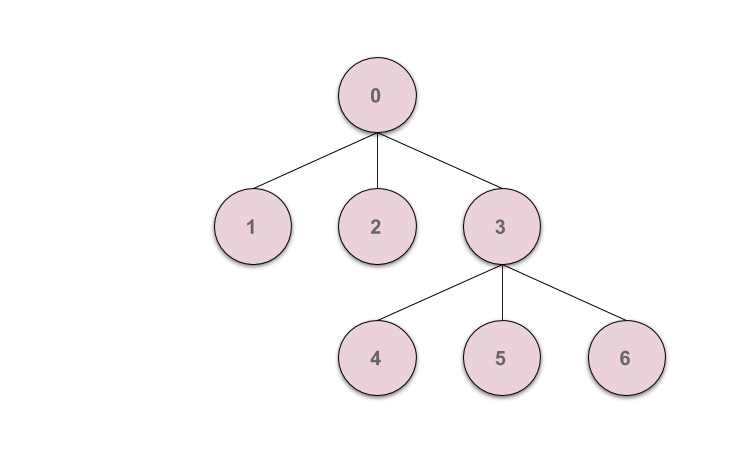
위의 Union 연산은 두 집합을 한쪽 방향으로 합치기 때문에 계속해서 Union연산을 수행하다보면 아래의 그림과 같이 한쪽으로 치우쳐진 Tree(skewed tree)형태가 만들어 질 수 있습니다.
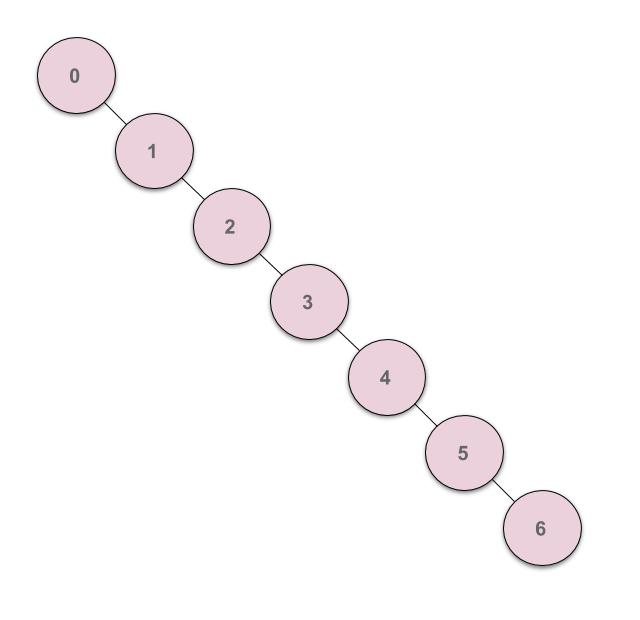
치우쳐진 Tree는 Linkedlist와 유사하게 작동하므로 $O(n)$의 시간복잡도를 갖습니다. 시간복잡도를 줄이려면 최적화가 필요합니다.

여기서 rank 의 개념을 도입시켜 Union 연산을 개선시킬 수 있습니다.
각각의 집합은 rank 를 갖습니다. rank 는 0의 초기값을 갖으며 rank 의 크기란 결국 tree의 높이를 나타냅니다.

def union(x, y):
  # rank should be initialized with 0
  x,y = find(x),find(y)
  if x != y:
    if rank[x] < rank[y]: parent[x] = y
    else: parent[y] = x
    if rank[x] == rank[y]: rank[y] += 1

Union 연산을 실행시에 Tree의 rank 즉 Tree의 높이가 낮은 노드에 subtree가 붙게됩니다.

Union연산 뿐만아니라 Find 연산 또한 개선하여 성능을 향상시킬 수 있습니다.
Find 연산은 여러번 수행 하더라도 최종 parent의 값은 변경이 되지 않는다는 성질이 있습니다.

위의 치우쳐진 Tree에서 find(6)을 실행하였을 때를 생각해 봅시다.
find(6)의 최종 Parent를 알고난 후에는 6의 Parent를 최종 Parent인 0으로 옮길 수 있습니다. 이렇게 하면 다음 find(6) call했을때에 결과를 바로 return 하게 됩니다. 또한 호출경로에 있는 find(5), find(4), find(3), find(2) 모두 최종 Parent에 직접 연결해 줄 수 있습니다. 이는 마치 Dynamic Programming의 Memorization과 유사하다고 볼 수 있습니다.

다음은 개선된 Find 연산입니다.

def find(x):
  if parent[x] != x:
    parent[x] = find(parent[x]) 
  return parent[x]

위의 치우쳐진 Tree에 대하여 6에 대한 Find연산의 결과는 다음 그림과 같습니다. 이렇게 되면 후의 Find연산에 대해 한번의 참조만으로 최종 Parent를 찾을 수 있습니다.

Finally

다음은 위의 (1,2), (3,6) Union연산에 이어서 (0,6)에 대한 Union연산의 결과입니다. find(6) 연산으로 노드6이 노드3에 붙게되고 0과 3이 Union됩니다.

위의 내용을 종합한 python code는 다음과 같습니다.